Advertisements
Advertisements
प्रश्न
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
पर्याय
50°
30°
60°
100°
उत्तर
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to 100°.
Explanation:

From ∆APB and ∆CPD,
∠APB = ∠CPD = 50° ...(Since they are vertically opposite angles)
`("AP")/("PD") = 6/5` ...(i)
Also, `("BP")/("CP") = 3/2.5`
Or `("BP")/("CP") = 6/5` ...(ii)
From equations (i) and (ii),
We get,
`("AP")/("PD") = ("BP")/("CP")`
So, ∆APB ∼ ∆DPC ...[Using SAS similarity criterion]
∴ ∠A = ∠D = 30° ...[Since, corresponding angles of similar triangles]
Since, Sum of angles of a triangle = 180°,
In ∆APB,
∠A + ∠B + ∠APB = 180°
So, 30° + ∠B + 50° = 180°
Then, ∠B = 180° – (50° + 30°)
∠B = 180° – 80° = 100°
Therefore, ∠PBA = 100°
APPEARS IN
संबंधित प्रश्न
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
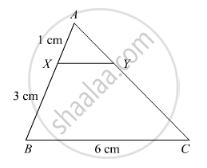
In the following figure, XY || BC. Find the length of XY.
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
