Advertisements
Advertisements
प्रश्न
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
उत्तर
Given, area of smaller triangle = 36 cm2
And area of larger triangle = 100 cm2
Also, length of a side of the larger triangle = 20 cm
Let length of the corresponding side of the smaller triangle = x cm
By property of area of similar triangle,
`("ar(larger triangle)")/("ar(smaller triangle)") = ("Side of larger triangle")^2/("Side of smaller triangle")^2`
⇒ `100/36 = (20)^2/x^2`
⇒ x2 = `((20)^2 xx 36)/100`
⇒ x2 = `(400 xx 36)/100` = 144
∴ x = `sqrt(144)` = 12 cm
Hence, the length of corresponding side of the smaller triangle is 12 cm.
APPEARS IN
संबंधित प्रश्न
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

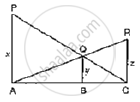
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
State the AAA-similarity criterion
In the given figure MN|| BC and AM: MB= 1: 2
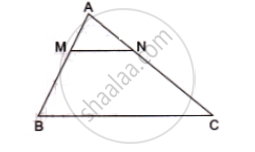
find ` (area(ΔAMN))/(area(ΔABC))`
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.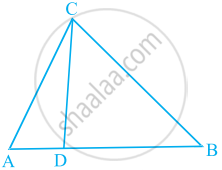
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
Which of the following conditions is not sufficient to determine the congruence of two triangles?
