Advertisements
Advertisements
प्रश्न
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
उत्तर
Given, area of smaller triangle = 36 cm2
And area of larger triangle = 100 cm2
Also, length of a side of the larger triangle = 20 cm
Let length of the corresponding side of the smaller triangle = x cm
By property of area of similar triangle,
`("ar(larger triangle)")/("ar(smaller triangle)") = ("Side of larger triangle")^2/("Side of smaller triangle")^2`
⇒ `100/36 = (20)^2/x^2`
⇒ x2 = `((20)^2 xx 36)/100`
⇒ x2 = `(400 xx 36)/100` = 144
∴ x = `sqrt(144)` = 12 cm
Hence, the length of corresponding side of the smaller triangle is 12 cm.
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
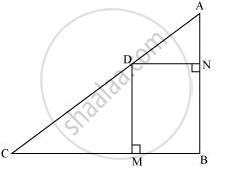
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
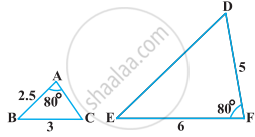
In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
The sides of certain triangles are given below. Determine which of them right triangles are.
1.6cm, 3.8cm, 4cm
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
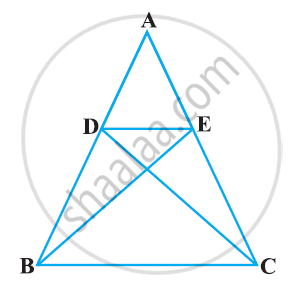
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
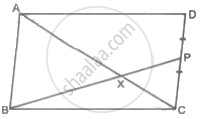
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
