Advertisements
Advertisements
प्रश्न
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
उत्तर
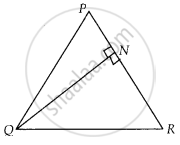
Given, ∆PQR,
N is a point on PR, such that QN ⊥ PR
And PN . NR = QN2
To prove: ∠PQR = 90°
Proof: We have, PN . NR = QN2
⇒ PN . NR = QN . QN
⇒ `("PN")/("QN") = ("QN")/("NR")` ...(i)
In ∆QNP and ∆RNQ,
`("PN")/("QN") = ("QN")/("NR")`
And ∠PNQ = ∠RNQ ...[Each equal to 90°]
∴ ∆QNP ~ ∆RNQ ...[By SAS similarity criterion]
Then, ∆QNP and ∆RNQ are equiangulars.
i.e., ∠PQN = ∠QRN
⇒ ∠RQN = ∠QPN
On adding both sides, we get
∠PQN + ∠RQN = ∠QRN + ∠QPN
⇒ ∠PQR = ∠QRN + ∠QPN ...(ii)
We know that, sum of angles of a triangle is 180°
In ∆PQR,
∠PQR + ∠QPR + ∠QRP = 180°
⇒ ∠PQR + ∠QPN + ∠QRN = 180° ...[∵ ∠QPR = ∠QPN and ∠QRP = ∠QRN]
⇒ ∠PQR + ∠PQR = 180° ...[Using equation (ii)]
⇒ 2∠PQR = 180°
⇒ ∠PQR = `180^circ/2` = 90°
∴ ∠PQR = 90°
Hence proved.
संबंधित प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
In the following figure, AB || QR. Find the length of PB.

ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that:
(i) ΔOMA and ΔOLC
(ii) `"OA"/"OC"="OM"/"OL"`
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
In figure, ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.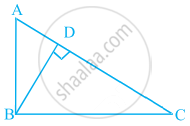
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
