Advertisements
Advertisements
प्रश्न
In the following figure, AB || QR. Find the length of PB.

उत्तर
We have, ΔPAB and ΔPQR
∠P = ∠P [common]
∠PAB = ∠PQR [corresponding angles]
Then, ΔPAB ~ ΔPQR [By AA similarity]
`therefore"PB"/"PR"="AB"/"QR"` [Corresponding parts of similar Δare proportional]
`rArr"PB"/6=3/9`
`rArr"PB"=3/9xx6=2` cm
APPEARS IN
संबंधित प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
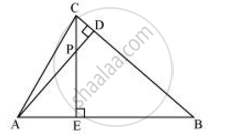
ΔAEP ∼ ΔCDP
In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
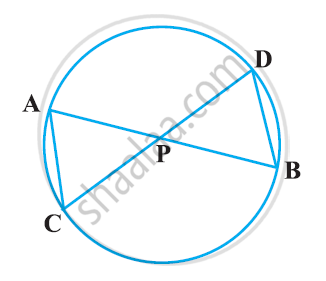
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

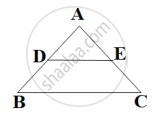
In the figure, if DE∥BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals ______.
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
