Advertisements
Advertisements
प्रश्न
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
उत्तर
Given, ratio of corresponding sides of two similar triangles = 2 : 3 or `2/3`
Area of smaller triangle = 48 cm2
By the property of area of two similar triangle,
Ratio of area of both triangles = (Ratio of their corresponding sides)2
i.e., `("ar(smaller triangle)")/("ar(larger triangle)") = (2/3)^2`
⇒ `48/("ar(larger triangle)") = 4/9`
⇒ ar(larger triangle) = `(48 xx 9)/4`
= 12 × 9
= 108 cm2
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
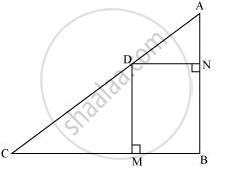
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
In the given figure MN|| BC and AM: MB= 1: 2
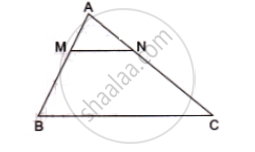
find ` (area(ΔAMN))/(area(ΔABC))`
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?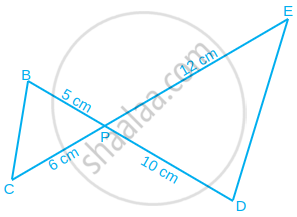
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
