Advertisements
Advertisements
प्रश्न
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.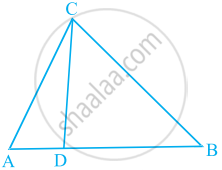
उत्तर
Given,
AC = 8 cm,
AD = 3 cm
And ∠ACB = ∠CDA
From figure,
∠CDA = 90°
∠ACB = ∠CDA = 90°
In right angled ΔADC,
AC2 = AD2 + CD2
⇒ (8)2 = (3)2 + (CD)2
⇒ 64 – 9 = CD2
⇒ CD = `sqrt(55)` cm
In ΔCDB and ΔADC,
∠BDC = ∠ADC ...[Each 90°]
∠DBC = ∠DCA ...[Each equal to 90° – ∠A]
∴ ΔCDB ∼ ΔADC
Then, `("CD")/("BD") = ("AD")/("CD")`
⇒ CD2 = AD × BD
∴ BD = `("CD"^2)/("AD")`
= `(sqrt(155))^2/3`
= `55/3` cm
APPEARS IN
संबंधित प्रश्न
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).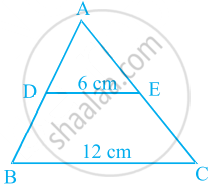
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ______.
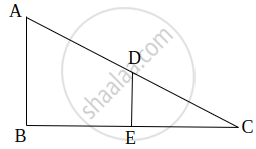
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?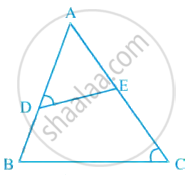
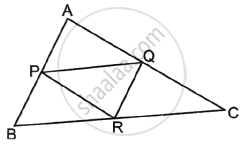
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.