Advertisements
Advertisements
प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
उत्तर
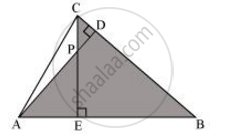
In ΔABD and ΔCBE
∠ADB = ∠CEB = 90°
∠ABD = ∠CBE ....(Common angle)
Hence, by using the AA similarity criterion,
ΔABD ∼ ΔCBE
APPEARS IN
संबंधित प्रश्न
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
In the given figure, value of x(in cm) is

In the figure, if DE∥BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals ______.
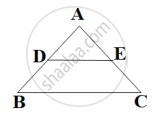
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
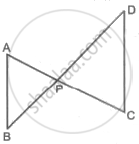
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.
Activity: In ΔABP and ΔCDP
`("AP")/("CP") = ("BP")/("DP")` ......`square`
∴ ∠APB ≅ `square` ......Vertically opposite angles
∴ `square` ∼ ΔCDP ....... `square` test of similarity.
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC
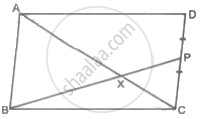
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

In the given figure, ΔLMN is similar to ΔPQR. To find the measure of ∠N, complete the following activity.
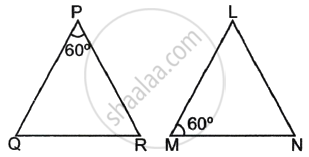
Given: ΔLMN ∼ ΔPQR
Since ΔLMN ∼ ΔPQR, therefore, corresponding angles are equal.
So, ∠L ≅ `square`
⇒ ∠L = `square`
We know, the sum of angles of a triangle = `square`
∴ ∠L + ∠M + ∠N = `square`
Substituting the values of ∠L and ∠M in equation (i),
`square` + `square` + ∠N = `square`
∠N + `square` = `square`
∠N = `square` – `square`
∠N = `square`
Hence, the measure of ∠N is `square`.
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
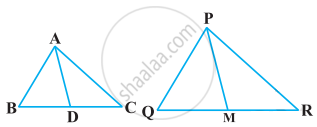
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.