Advertisements
Advertisements
प्रश्न
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
उत्तर
When two triangles are similar, then the ratios of the lengths of their corresponding sides are equal.
Here, ΔABC ~ΔDEF
∴ `(AB)/(DE)=(BC)/(EF)`
⇒`( AB)/(2AB)=(6)/(EF)`
⇒ EF = 12 cm
APPEARS IN
संबंधित प्रश्न
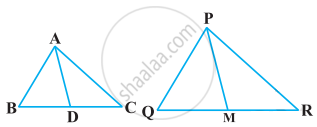
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
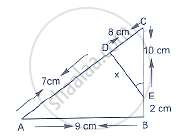
In below figure, ∠A = ∠CED, Prove that ΔCAB ~ ΔCED. Also, find the value of x.
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ∼ ΔPQR, then prove that ΔAMC ∼ ΔPNR.
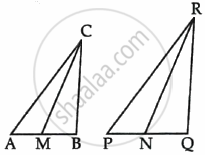
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.