Advertisements
Advertisements
प्रश्न
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
उत्तर
We know that, the sum of three angles of a triangle is 180°.

In ∆PQR,
∠P + ∠Q + ∠R = 180°
⇒ 55° + 25° + ∠R = 180°
⇒∠R = 180° – (55° + 25°)
= 180° – 80°
= 100°
In ∆TSM,
∠T + ∠S + ∠M = 180°
⇒ ∠T + ∠25° + 100° = 180°
⇒ ∠T = 180° – (25° + 100°)
= 180° – 125°
= 55°
In ∆PQR and ∆TSM,
∠P = ∠T,
∠Q = ∠S
And ∠R = ∠M
∴ ∠PQR = ∠TSM ...[Since, all corresponding angles are equal]
Hence, ∆QPR is not similar to ∆TSM, since correct correspondence is P `↔` T, Q `↔` S and R `↔` M.
APPEARS IN
संबंधित प्रश्न
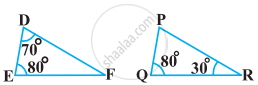
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
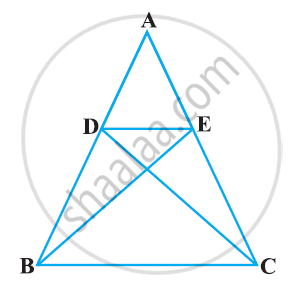
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
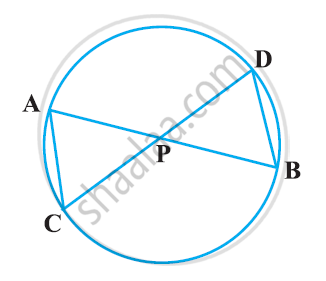
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
It is given that ΔABC ~ ΔDFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true ______.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

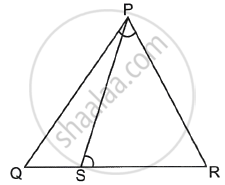
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
Which of the following is NOT a similarity criterion of traingles?
