Advertisements
Advertisements
प्रश्न
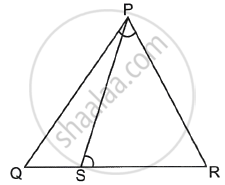
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
उत्तर
Given: ∠QPR = ∠PSR
In ΔQPR and ΔPSR,
∠QRP ≅ ∠PRS ......[Common angle]
∠QPR ≅ ∠PSR ......[Given]
So, according to the AA similarity criterion,
ΔQPR ∼ ΔPSR
∴ `(QR)/(PR) = (PR)/(SR)` .......[C.S.S.T.]
⇒ QR × SR = PR2
Hence proved.
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

In below figure, ∠A = ∠CED, Prove that ΔCAB ~ ΔCED. Also, find the value of x.
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
The sides of certain triangles are given below. Determine which of them right triangles are.
1.6cm, 3.8cm, 4cm
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
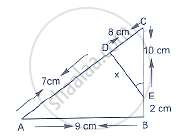
In the given figure, value of x(in cm) is

Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
It is given that ΔABC ~ ΔDFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true ______.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
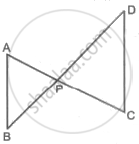
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.
Activity: In ΔABP and ΔCDP
`("AP")/("CP") = ("BP")/("DP")` ......`square`
∴ ∠APB ≅ `square` ......Vertically opposite angles
∴ `square` ∼ ΔCDP ....... `square` test of similarity.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

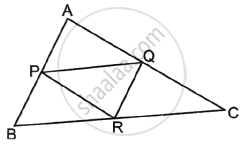
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

Which of the following is NOT a similarity criterion of traingles?
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.