Advertisements
Advertisements
प्रश्न
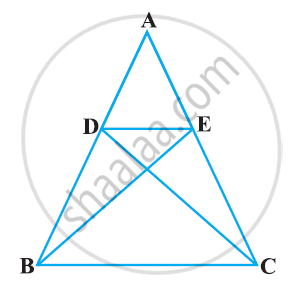
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
उत्तर
It is given that ΔABE ≅ ΔACD.
∴ AB = AC …(1) [CPCT]
And, AD = AE …(2) [CPCT]
⇒ `"AE"/"AB" = "AD"/"AC"` ...(3)
In ΔADE and ΔABC,
∵ `"AE"/"AB" = "AD"/"AC"` ...[Dividing equation 2 by 1]
∠A = ∠A ...[Common angle]
∴ ΔADE ∼ ΔABC ...[By SAS similarity criterion]
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
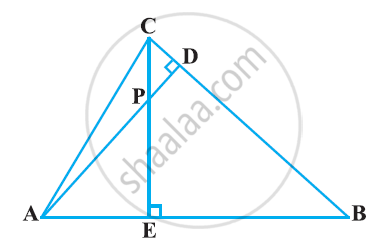
ΔAEP ∼ ΔADB
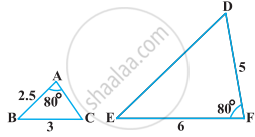
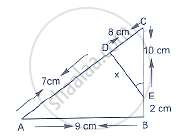
In below figure, ∠A = ∠CED, Prove that ΔCAB ~ ΔCED. Also, find the value of x.
In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that:
(i) ΔOMA and ΔOLC
(ii) `"OA"/"OC"="OM"/"OL"`
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

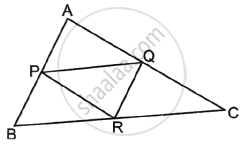
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
Which of the following is NOT a similarity criterion of traingles?
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.
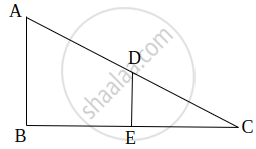
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
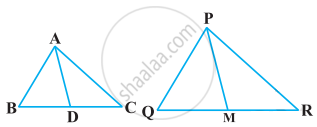
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.