Advertisements
Advertisements
प्रश्न
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
उत्तर
We know that, the sum of three angles of a triangle is 180°.

In ∆PQR,
∠P + ∠Q + ∠R = 180°
⇒ 55° + 25° + ∠R = 180°
⇒∠R = 180° – (55° + 25°)
= 180° – 80°
= 100°
In ∆TSM,
∠T + ∠S + ∠M = 180°
⇒ ∠T + ∠25° + 100° = 180°
⇒ ∠T = 180° – (25° + 100°)
= 180° – 125°
= 55°
In ∆PQR and ∆TSM,
∠P = ∠T,
∠Q = ∠S
And ∠R = ∠M
∴ ∠PQR = ∠TSM ...[Since, all corresponding angles are equal]
Hence, ∆QPR is not similar to ∆TSM, since correct correspondence is P `↔` T, Q `↔` S and R `↔` M.
APPEARS IN
संबंधित प्रश्न
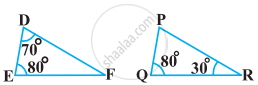
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
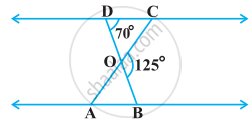
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
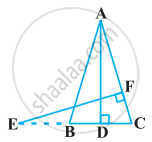
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
In the following figure, AB || QR. Find the length of PB.

In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

Two triangles DEF an GHK are such that ∠D = 48° and ∠H = 57° . If ΔDEF ∼GHK then find the measures of ∠F
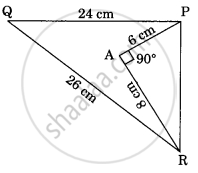
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

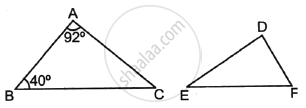
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?