Advertisements
Advertisements
प्रश्न
In the given figure MN|| BC and AM: MB= 1: 2
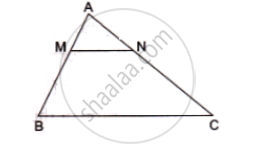
find ` (area(ΔAMN))/(area(ΔABC))`
उत्तर
We have
AM : MB = 1 : 2
⇒ AM:MB=1:2
⇒ `(MB)/(AM)=2/1`
Adding 1 to both sides, we get
⇒`( MB)/(AM)+1=2/1+1`
⇒`(MB+AM)/(AM)=(2+1)/1`
⇒ `(AB)/(AM)=3/1`
Now, In ΔAMN and ΔABC
∠𝐴𝑀𝑁 = ∠𝐴𝐵𝐶 (𝐶𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑎𝑛𝑔𝑙𝑒𝑠 𝑖𝑛 𝑀𝑁 ∥ 𝐵𝐶)
∠𝐴𝑁𝑀 = ∠𝐴𝐶𝐵 (𝐶𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑎𝑛𝑔𝑙𝑒𝑠 𝑖𝑛 𝑀𝑁 ∥ 𝐵𝐶)
By AA similarity criterion, ΔAMN ~ Δ ABC
If two triangles are similar, then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
∴`( area (Δ AMN))/(area(ΔABC))=((AM)/(AB))^2=(1/3)^2=1/9`
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
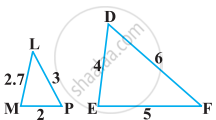
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
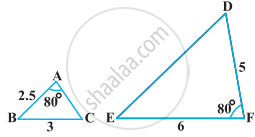
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that:
(i) ΔOMA and ΔOLC
(ii) `"OA"/"OC"="OM"/"OL"`
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.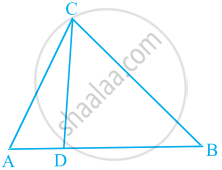
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ______.
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal ______.
