Advertisements
Advertisements
प्रश्न
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
उत्तर

In Δ AOB and COD
∠𝐴𝐵𝑂= ∠𝐶𝐷𝑂 (𝐴𝑙𝑡𝑒𝑟𝑛𝑡𝑒 𝑎𝑛𝑔𝑙𝑒𝑠 𝑖𝑛 𝐴𝐵∥𝐶𝐷)
∠𝐴𝑂𝐵= ∠𝐶𝑂𝐷 (𝑉𝑒𝑟𝑡𝑖𝑐𝑎𝑙𝑙𝑦 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑎𝑛𝑔𝑙𝑒𝑠)
By AA similarity criterion, ΔAOB ~ ΔCOD
If two triangles are similar, then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
∴ `(area (Δ AOB))/(area(Δ COD))=((AB)/(CD))^2`
⇒ `84/(area(ΔCOD))=((2CD)/(CD))^2`
⇒` area (Δ COD)=12 cm^2`
APPEARS IN
संबंधित प्रश्न
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
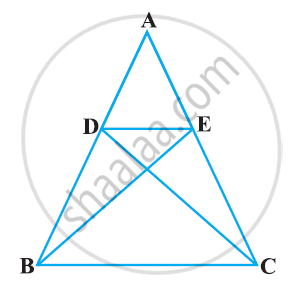
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
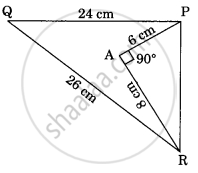
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
Which of the following conditions is not sufficient to determine the congruence of two triangles?
If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal ______.
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
