Advertisements
Advertisements
प्रश्न
In a ΔABC, D and E are points on AB and AC respectively such that DE || BC. If AD = 2.4cm, AE = 3.2 cm, DE = 2cm and BC = 5 cm, find BD and CE.
उत्तर
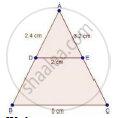
We have,
DE || BC
Now, In ΔADE and ΔABC
∠A = ∠A [common]
∠ADE = ∠ABC [∵ DE || BC ⇒ Corresponding angles are equal]
⇒ ΔADE ~ ΔABC [By AA criteria]
`rArr"AB"/"BC"="AD"/"DE"`
`rArr"AB"=(2.4xx5)/2`
⇒ AB = 1.2 × 5 = 6.0 cm
⇒ AB = 6 cm
∴ BD = 6 cm
BD = AB – AD
= 6 – 2.4 = 3.6 cm
⇒ DB = 3.6 cm
Now,
`"AC"/"BC"="AE"/"DE"` [∵ Corresponding sides of similar triangles are equal]
`rArr"AC"/5=3.2/2`
`rArr"AC"=(3.2xx5)/2=1.6xx5=8.0 ` cm
⇒ AC = 8 cm
∴ CE = AC – AE
= 8 – 3.2 = 4.8 cm
Hence, BD = 3.6 cm and CE = 4.8 cm
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
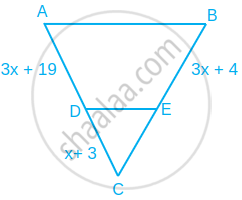
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

In the given figure, O is a point inside a ΔPQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ΔPQR is right-angled.
Find the length of a diagonal of a rectangle whose adjacent sides are 30cm and 16cm.
In a ABC , AD is a median and AL ⊥ BC .
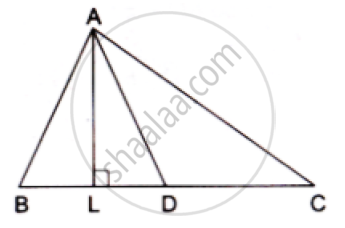
Prove that
(a) `AC^2=AD^2+BC DL+((BC)/2)^2`
(b) `AB^2=AD^2-BC DL+((BC)/2)^2`
(c) `AC^2+AB^2=2.AD^2+1/2BC^2`
State and converse of Thale’s theorem.
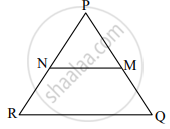
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
Find the value of x for which DE || AB in figure.