Advertisements
Advertisements
प्रश्न
Find the value of x for which DE || AB in figure.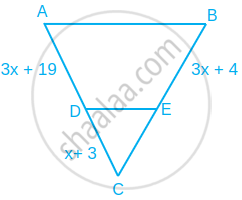
उत्तर
According to the question,
DE || AB
Using basic proportionality theorem,
`("CD")/("AD") = ("CE")/("BE")`
∴ If a line is drawn parallel to one side of a triangle such that it intersects the other sides at distinct points, then, the other two sides are divided in the same ratio.
Hence, we can conclude that, the line drawn is equal to the third side of the triangle.
⇒ `(x + 3)/(3x + 19) = x/(3x + 4)`
(x + 3)(3x + 4) = x(3x + 19)
3x2 + 4x + 9x + 12 = 3x2 + 19x
19x – 13x = 12
6x = 12
∴ x = `12/6` = 2
APPEARS IN
संबंधित प्रश्न
In below Fig., state if PQ || EF.
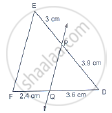
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

State and converse of Thale’s theorem.
State the midpoint theorem
In fig, seg DE || sec BC, identify the correct statement.

ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
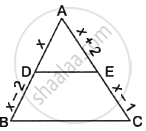
In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.