Advertisements
Advertisements
Question
Find the value of x for which DE || AB in figure.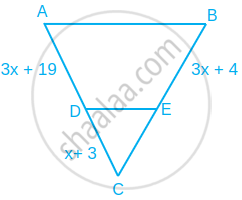
Solution
According to the question,
DE || AB
Using basic proportionality theorem,
`("CD")/("AD") = ("CE")/("BE")`
∴ If a line is drawn parallel to one side of a triangle such that it intersects the other sides at distinct points, then, the other two sides are divided in the same ratio.
Hence, we can conclude that, the line drawn is equal to the third side of the triangle.
⇒ `(x + 3)/(3x + 19) = x/(3x + 4)`
(x + 3)(3x + 4) = x(3x + 19)
3x2 + 4x + 9x + 12 = 3x2 + 19x
19x – 13x = 12
6x = 12
∴ x = `12/6` = 2
APPEARS IN
RELATED QUESTIONS
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=3/4` and AC = 15 cm, find AE
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
In fig, seg DE || sec BC, identify the correct statement.

In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.
ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
