Advertisements
Advertisements
प्रश्न
M and N are points on the sides PQ and PR respectively of a ΔPQR. For the following case, state whether MN || QR
PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
उत्तर
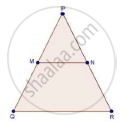
We have, PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
Hence,
`"PM"/"QM"=4/4.5=8/9`
Also,
`"PN"/"NR"=4/4.5=8/9`
Hence, `"PM"/"QM"="PN"/"NR"`
By converse of proportionality theorem
MN || QR
APPEARS IN
संबंधित प्रश्न
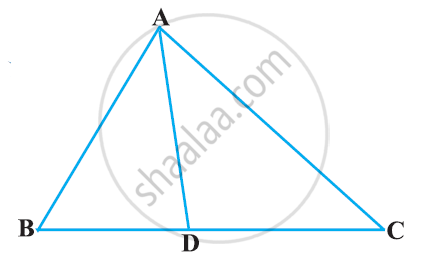
In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
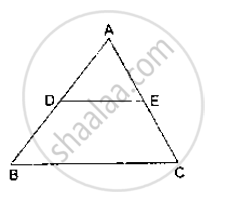
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=2/3` and AC = 18 cm, find AE
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In below Fig., state if PQ || EF.
In the adjoining figure, ABC is a triangle in which AB = AC. IF D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.
In a ABC , AD is a median and AL ⊥ BC .
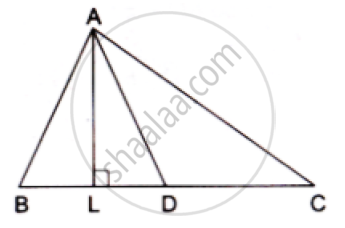
Prove that
(a) `AC^2=AD^2+BC DL+((BC)/2)^2`
(b) `AB^2=AD^2-BC DL+((BC)/2)^2`
(c) `AC^2+AB^2=2.AD^2+1/2BC^2`
State and converse of Thale’s theorem.
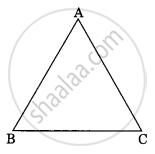
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
Find the value of x for which DE || AB in figure.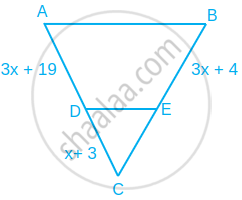
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
