Advertisements
Advertisements
प्रश्न
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
उत्तर
According to the question,
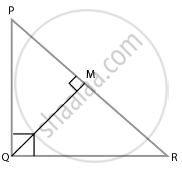
In ∆PQR,
PR2 = QR2 and QM ⊥ PR
Using Pythagoras theorem, we have,
PR2 = PQ2 + QR2
∆PQR is right-angled triangle at Q.
From ∆QMR and ∆PMQ, we have,
∠M = ∠M
∠MQR = ∠QPM ...[= 90° – ∠R]
So, using the AAA similarity criteria,
We have,
∆QMR ∼ ∆PMQ
Also, we know that,
Area of triangles = `1/2` × base × height
So, by property of area of similar triangles,
⇒ `("ar(∆QMR)")/("ar(PMQ)") = ("QM")^2/("PM")^2`
⇒ `("ar(∆QMR)")/("ar(PMQ)") = (1/2 xx "RM" xx "QM")/(1/2 xx "PM" xx "QM")`
⇒ `("ar(∆QMR)")/("ar(PMQ)") = ("QM")^2/("PM")^2`
QM2 = PM × RM
Hence proved.
APPEARS IN
संबंधित प्रश्न
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In the following figure, AB || QR. Find the length of PB.

ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
State the AAA-similarity criterion
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ______.
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?
ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

