Advertisements
Advertisements
प्रश्न
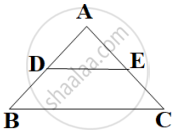
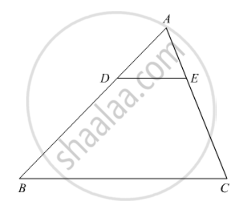
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?
पर्याय
x = `(a + b)/(ay)`
y = `(ax)/(a + b)`
x = `(ay)/(a + b)`
`x/y = a/b`
उत्तर
x = `(ay)/(a + b)`
Explanation:

In ΔADE and ΔABC
ΔADE = ΔABC ......(Corresponding angle)
∠A = ∠A ......(Common)
∴ ΔADE ∼ ΔABC ....(AA similarity criterion)
Now, `(AD)/(AB) = (DE)/(BC) = (AE)/(AC)`
`(DE)/(BC) = (AE)/(AC)`
`x/y = a/(a + b)`
x = `(ay)/(a + b)`
APPEARS IN
संबंधित प्रश्न
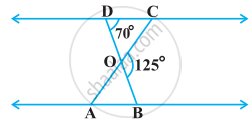
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
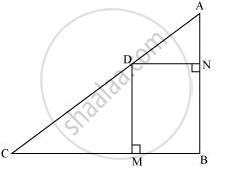
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
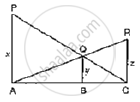
In the following figure, PA, QB and RC are each perpendicular to AC. Prove that `1/x+1/z=1/y`
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
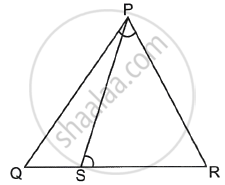
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.