Advertisements
Advertisements
प्रश्न
It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
उत्तर
We know that,
Corresponding angles are equal in similar triangles.
So, we get,
∠D = ∠R
∠E = ∠P
∠F = ∠Q
APPEARS IN
संबंधित प्रश्न
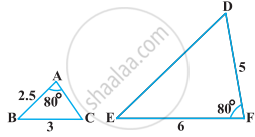
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
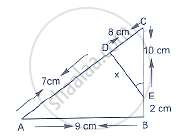
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
In below figure, ∠A = ∠CED, Prove that ΔCAB ~ ΔCED. Also, find the value of x.
The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
In the given figure, ΔLMN is similar to ΔPQR. To find the measure of ∠N, complete the following activity.
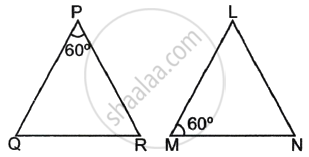
Given: ΔLMN ∼ ΔPQR
Since ΔLMN ∼ ΔPQR, therefore, corresponding angles are equal.
So, ∠L ≅ `square`
⇒ ∠L = `square`
We know, the sum of angles of a triangle = `square`
∴ ∠L + ∠M + ∠N = `square`
Substituting the values of ∠L and ∠M in equation (i),
`square` + `square` + ∠N = `square`
∠N + `square` = `square`
∠N = `square` – `square`
∠N = `square`
Hence, the measure of ∠N is `square`.
