Advertisements
Advertisements
प्रश्न
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
उत्तर
We have: ∠C = 90° and CD ⊥ AB
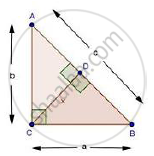
In ΔACB and ΔCDB
∠B = ∠B [common]
∠ACB = ∠CDB [Each 90°]
Then, ΔACB ~ ΔCDB [By AA similarity]
`therefore"AC"/"CD"="AB"/"CB"` [Corresponding parts of similar Δ are proportional]
`rArrb/x=c/a`
⇒ ab = cx
APPEARS IN
संबंधित प्रश्न
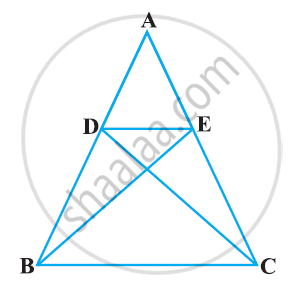
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

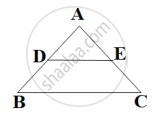
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
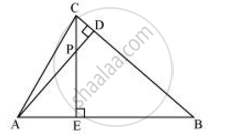
ΔAEP ∼ ΔCDP
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
State the two properties which are necessary for given two triangles to be similar.
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
In the figure, if DE∥BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals ______.
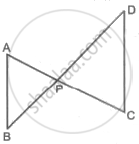
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.
Activity: In ΔABP and ΔCDP
`("AP")/("CP") = ("BP")/("DP")` ......`square`
∴ ∠APB ≅ `square` ......Vertically opposite angles
∴ `square` ∼ ΔCDP ....... `square` test of similarity.
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

