Advertisements
Advertisements
Question
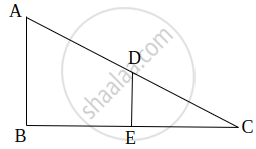
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
Solution
We have: ∠C = 90° and CD ⊥ AB
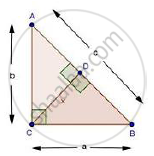
In ΔACB and ΔCDB
∠B = ∠B [common]
∠ACB = ∠CDB [Each 90°]
Then, ΔACB ~ ΔCDB [By AA similarity]
`therefore"AC"/"CD"="AB"/"CB"` [Corresponding parts of similar Δ are proportional]
`rArrb/x=c/a`
⇒ ab = cx
APPEARS IN
RELATED QUESTIONS
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

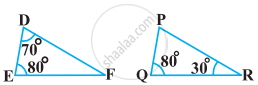
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
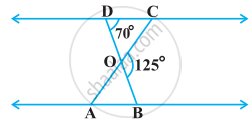
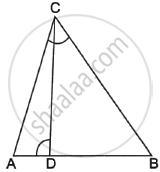
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
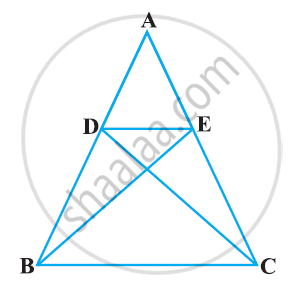
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
In the given figure, ∠ADC = ∠BCA; prove that ΔACB ∼ ΔADC. Hence find BD if AC = 8 cm and AD = 3 cm.
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.
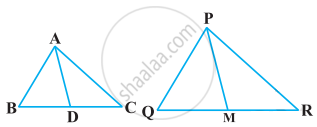
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.