Advertisements
Advertisements
प्रश्न
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

उत्तर
Given:
◻ABCD is a parallelogram.
E is a point on side BC.
Line DE intersects ray AB in point T.
To prove: DE × BE = CE × TE
Proof: In ∆BET and ∆CED
∠BET = ∠CED ...(Vertically opposite angles)
∠BTE = ∠CDE ...(Alternate interior angles, AB || CD and DT is a transversal line)
By AA test of similarity,
∆BET ∼ ∆CED
∴
∴ DE × BE = CE × TE
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6cm, AD = 1.4cm, AC= 7.2 cm and AE = 1.8 cm.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
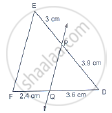
In below Fig., state if PQ || EF.
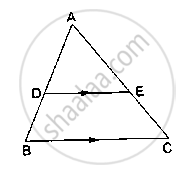
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If
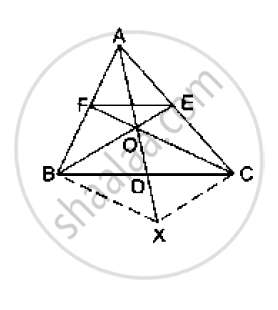
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ΔABE and ΔACD.
In a ABC , AD is a median and AL ⊥ BC .
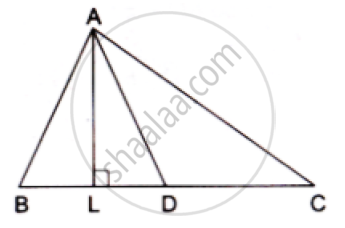
Prove that
(a)
(b)
(c)
State the basic proportionality theorem.
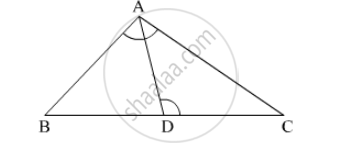
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
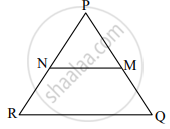
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
In ΔABC, AB = 6 cm and DE || BC such that AE =
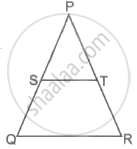
In the given figure, Sand Tare points on sides PQ and PR, respectively of ΔPQR such that ST is parallel to QR and SQ = TR. Prove that ΔPQR is an isosceles triangles.