Advertisements
Advertisements
Question
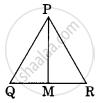
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
Solution
When two triangles are similar, then the ratios of the lengths of their corresponding sides are proportional.
Here, ΔBMP ~ ΔCNR
∴` (BM)/(CN)=(BP)/(CR)=(MP)/(NR)` ...........(1)
NOW`(BM)/(CN)=(MP)/(NR)` [𝑈𝑠𝑖𝑛𝑔 (1)]
⇒ `CN=(BMxxNR)/(MP)=(9xx9)/6=13.5 cm`
𝐴𝑔𝑎𝑖𝑛, `(BM)/(CN)=(BP)/(CR)` [𝑈𝑠𝑖𝑛𝑔 (1)]
⇒ `CR=(BPxxCN)/(BM)=(5xx13.5)/9=7.5 cm`
Perimeter of ΔCNR = CN + NR + CR = 13.5 + 9 + 7.5 = 30 cm
APPEARS IN
RELATED QUESTIONS
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = x cm, DB = (x – 2) cm, AE = (x + 2) cm and EC = (x – 1) cm.
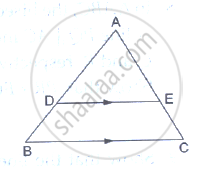
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

Each of the equal sides of an isosceles triangle is 25 cm. Find the length of its altitude if the base is 14 cm.
In fig, seg DE || sec BC, identify the correct statement.

In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.
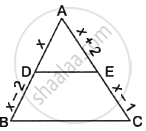
In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`