Advertisements
Advertisements
प्रश्न
If ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm and BC = 15 cm, then PR is equal to ______.
विकल्प
10 cm
12 cm
`20/3` cm
8 cm
उत्तर
If ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm and BC = 15 cm, then PR is equal to 10 cm.
Explanation:
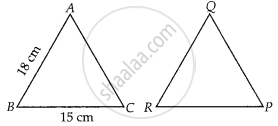
Given, ∆ABC ~ ∆QRP,
AB = 18 cm
And BC = 15 cm
We know that, the ratio of the area of two similar triangles is equal to the ratio of square of their corresponding sides.
∴ `("ar(∆ABC)")/("ar(∆QRP)") = ("BC")^2/("RP")^2`
But, `("ar(∆ABC)")/("ar(∆PQR)") = 9/4` ...[Given]
⇒ `(15)^2/("RP")^2 = 9/4` ...[∵ BC = 15 cm, given]
⇒ (RP)2 = `(225 xx 4)/9` = 100
∴ RP = 10 cm
APPEARS IN
संबंधित प्रश्न
In figure, `\frac{AO}{OC}=\frac{BO}{OD}=\frac{1}{2}` and AB = 5 cm. Find the value of DC.
A vertical stick 20 cm long casts a shadow 6 cm long on the ground. At the same time, a tower casts a shadow 15 m long on the ground. Find the height of the tower.
In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
State, true or false:
All equiangular triangles are similar.
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that: `(FB)/(AD) = (BC)/(ED)`.

The perimeter of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
On a map, drawn to a scale of 1 : 250000, a triangular plot PQR of land has the following measurements :
PQ = 3cm, QR = 4 cm and angles PQR = 90°
(i) the actual lengths of QR and PR in kilometer.
(ii) the actual area of the plot in sq . km.
In the given figure, DB⊥BC, DE⊥AB and AC⊥BC.
Prove that `(BE)/(DE)=(AC)/(BC)`

State the AA-similarity criterion
Figure shows Δ KLM , P an T on KL and KM respectively such that∠ KLM =∠ KTP.
If `"KL"/"KT" = 9/5` , find `("Ar" triangle "KLM")/("Ar" triangle "KTP")`.

In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
In MBC, DE is drawn parallel to BC. If AD: DB=2:3, DE =6cm and AE =3.6cm, find BC and AC.
The actual area of an island is 1872km2 . On a map, this area is 117 cm2. if the length of the coastline is 44cm on the map, find the length of its actual coastline.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4, AE = 8, DB = x - 4 and EC = 3x - 19, find x.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3,Find x.
In ΔABC, BP and CQ are altitudes from B and C on AC and AB respectively. BP and CQ intersect at O. Prove that
(i) PC x OQ = QB x OP
(ii) `"OC"^2/"OB"^2 = ("PC" xx "PO")/("QB" xx "QO")`
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate: Length of AB, if A'B' = 5.4cm
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The area of the plot in sq km
Check whether the triangles are similar and find the value of x
In the adjacent figure ∠BAC = 90° and AD ⊥ BC then

D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
In the given figure YH || TE. Prove that ΔWHY ~ ΔWET and also find HE and TE
A flag pole 15 m high casts a shadow of 3 m at 10 a.m. The shadow cast by a building at the same time is 18.6 m. The height of the building is
ΔABC ~ ΔDEF. Write the ratios of their corresponding sides
In ∠BAC = 90° and AD ⊥ BC. A then ______.

∆ABC ~ ∆PQR. If AM and PN are altitudes of ΔABC and ∆PQR respectively and AB2 : PQ2 = 4 : 9, then AM : PN = ______.
In figure, if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.

In ΔPQR, S and T are points on PQ and PR respectively. `(PS)/(SQ) = (PT)/(TR)` and ∠PST = ∠PRQ. Prove that PQR is an isosceles triangle.
