Advertisements
Advertisements
प्रश्न
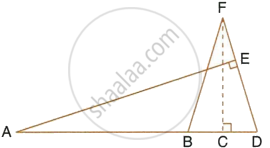
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that: `(FB)/(AD) = (BC)/(ED)`.
उत्तर
Given, FB = FD
∴ ∠FDB = ∠FBD ...(1)
In ΔAED = ΔFCB,
∠AED = ∠FCB = 90°
∠ADE = ∠FBC ...[Using (1)]
ΔAED ~ ΔFCB ...[By AA similarity]
∴ `(AD)/(FB) = (ED)/(BC)`
`(FB)/(AD) = (BC)/(ED)`
APPEARS IN
संबंधित प्रश्न
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
AD and BC are two straight lines intersecting at 0. CD and BA are perpendirulars from Band Con AD. If AB=6cm, CD =9cm, AD =20cm and BC=25cm, find the lengths of AO, BO, CO and DO.
A ship is 400m laig and 100m wide. The length of its model is 20 cm. find the surface area of the deck of the model.
A model of a ship is made with a scale factor of 1 : 500. Find
The volume of the ship, if the volume of its model is 200 cm3.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AD)/(AB)`
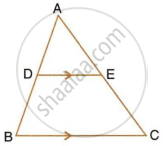
A line segment DE is drawn parallel to base BC of ΔABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE.
Sides of a triangle are 7, 24 and 25. Determine whether the triangle is a right-angled triangle or not.
ABCD is a parallelogram whose sides AB and BC are 18cm and 12cm respectively. G is a point on AC such that CG : GA = 3 : 5 BG is produced to meet CD at Q and AD produced at P. Prove that ΔCGB ∼ ΔAGP. Hence, fi AP.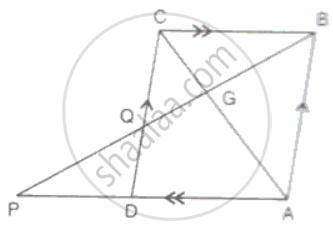
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
On a map drawn to a scale of 1:25000, a triangular plot of land is right angled and the sides forming the right angle measure 225cm and 64cm.Find: The area of the plot in sq. km.
