Advertisements
Advertisements
प्रश्न
A line segment DE is drawn parallel to base BC of ΔABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE.
उत्तर
In ΔABC
DE || BC
AB = 5BD, EC = 3.2 cm
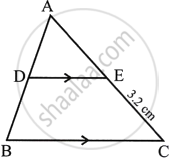
To find AE
Since, DE || BC
∴ ΔADE ∼ ΔABC
Since a line drawn parallel to one side of triangle divides the other sides proportionality.
∴ `(AD)/(AB) = (AE)/(EC)` ...`{{:(∵ (AB)/(BD) = 5/1),(\implies (BD)/(AB) = 1/5),(AD = AB - BD = 5 - 1 = 4),(∴ (AD)/(DB) = 4/1):}}`
`\implies 4/1 = (AE)/3.2`
`\implies AE = (4 xx 3.2)/1`
= `12.8/1`
= 12.8 cm
APPEARS IN
संबंधित प्रश्न
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:

- ΔEGD ~ ΔCGB and
- BG = 2GD from (i) above.
State the SSS-similarity criterion for similarity of triangles
Are the triangles in the given figure similar? If yes, by which test?

Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`

Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD : BD = 4 : 5 and EC = 2.5cm, find AE.
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate:Length of B' C', if BC = 8cm
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆RPN

In the given figure, UB || AT and CU ≡ CB Prove that ΔCUB ~ ΔCAT and hence ΔCAT is isosceles.
