Advertisements
Advertisements
Question
A line segment DE is drawn parallel to base BC of ΔABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE.
Solution
In ΔABC
DE || BC
AB = 5BD, EC = 3.2 cm
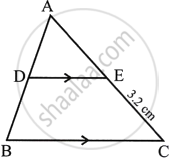
To find AE
Since, DE || BC
∴ ΔADE ∼ ΔABC
Since a line drawn parallel to one side of triangle divides the other sides proportionality.
∴ `(AD)/(AB) = (AE)/(EC)` ...`{{:(∵ (AB)/(BD) = 5/1),(\implies (BD)/(AB) = 1/5),(AD = AB - BD = 5 - 1 = 4),(∴ (AD)/(DB) = 4/1):}}`
`\implies 4/1 = (AE)/3.2`
`\implies AE = (4 xx 3.2)/1`
= `12.8/1`
= 12.8 cm
APPEARS IN
RELATED QUESTIONS
In ∆ABC, DE is parallel to base BC, with D on AB and E on AC. If `\frac{AD}{DB}=\frac{2}{3}` , find `\frac{BC}{DE}.`
In the given figure, ΔODC~ΔOBA, ∠BOC = 115° and ∠CDO = 700.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.

The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
In ΔPQR, PQ = 10 cm, QR = 12cm, PR = 8 cm, find the biggest and the smallest angle of the triangle.
In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`

In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find : PQ

Given that ΔABC ∼ ΔPRQ, name the corresponding angles and the corresponding sides.
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate: Length of AB, if A'B' = 5.4cm
In the given figure, UB || AT and CU ≡ CB Prove that ΔCUB ~ ΔCAT and hence ΔCAT is isosceles.
If ΔABC ~ ΔLMN and ∠B = 40°, then ∠M = ? Give reason.
