Advertisements
Advertisements
Question
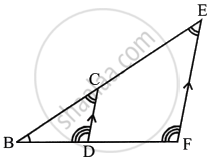
In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.

Solution
i. In ΔACB and ΔFCE, we have
∠ACB = ∠FCE ...(Vertically opposite angles)
∠CBA = ∠CEF ...(Alternate angles)
∴ ΔACB ∼ ΔFCE ...(AA axiom of similarity)
Thus their corresponding sides are proportional.
∴ `(AB)/(BC) = (EF)/(EC)`
`\implies (7.5 cm)/(x cm) = (4.5 cm)/(3 cm)`
`\implies x = ((7.5 xx 3)/4.5) cm`
= `225/45 cm`
= 5 cm
ii. In ΔEBF and ΔCBD, we have
∠B = ∠B ...(Common angle)
∠EFB = ∠CDB ...(Corresponding angles)
∠BEF = ∠BCD
∴ ΔEBF ∼ ΔCBD ...(AA axiom of similarity)
Thus, `(EB)/(CB) = (EF)/(CD)`
`\implies (EC + CB)/(CB) = (4.5 cm)/(y cm)`
`\implies (3 + x)/x = 4.5/y`
`\implies ((3 + 5) cm)/(5 cm) = 4.5/y`
`\implies y = (4.5 xx 5)/8`
= `45/16 cm`
= `2 13/16 cm`
APPEARS IN
RELATED QUESTIONS
See the given figure. DE || BC. Find AD.

In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In the given figure, ΔOAB ~ ΔOCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate : the area of the plot in sq. km.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AD)/(AB)`

In the given figure, AB and DE are perpendicular to BC.

- Prove that ΔABC ∼ ΔDEC
- If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
- Find the ratio of the area of a ΔABC : area of ΔDEC.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
Construct a triangle similar to a given triangle PQR with its sides equal to `7/3` of the corresponding sides of the triangle PQR (scale factor `7/3 > 1`)
In fig. BP ⊥ AC, CQ ⊥ AB, A−P−C, and A−Q−B then show that ΔAPB and ΔAQC are similar.
In ΔAPB and ΔAQC
∠APB = [ ]° ......(i)
∠AQC = [ ]° ......(ii)
∠APB ≅ ∠AQC .....[From (i) and (ii)]
∠PAB ≅ ∠QAC .....[______]
ΔAPB ~ ΔAQC .....[______]
