Advertisements
Advertisements
प्रश्न
A line segment DE is drawn parallel to base BC of ΔABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE.
उत्तर
In ΔABC
DE || BC
AB = 5BD, EC = 3.2 cm
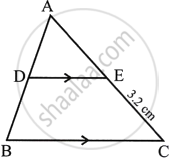
To find AE
Since, DE || BC
∴ ΔADE ∼ ΔABC
Since a line drawn parallel to one side of triangle divides the other sides proportionality.
∴ `(AD)/(AB) = (AE)/(EC)` ...`{{:(∵ (AB)/(BD) = 5/1),(\implies (BD)/(AB) = 1/5),(AD = AB - BD = 5 - 1 = 4),(∴ (AD)/(DB) = 4/1):}}`
`\implies 4/1 = (AE)/3.2`
`\implies AE = (4 xx 3.2)/1`
= `12.8/1`
= 12.8 cm
APPEARS IN
संबंधित प्रश्न
In figure, `\frac{AO}{OC}=\frac{BO}{OD}=\frac{1}{2}` and AB = 5 cm. Find the value of DC.
D is a point on the side BC of ∆ABC such that ∠ADC = ∠BAC. Prove that` \frac{"CA"}{"CD"}=\frac{"CB"}{"CA"} or "CA"^2 = "CB" × "CD".`
In figure, ∠BAC = 90º and segment AD ⊥ BC. Prove that AD2 = BD × DC.
The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm, what is the corresponding side of the other triangle?
In ΔABC, D and E are the midpoints of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.

The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
A model of a ship is made to a scale 1 : 300.
- The length of the model of the ship is 2 m. Calculate the length of the ship.
- The area of the deck of the ship is 180,000 m2. Calculate the area of the deck of the model.
- The volume of the model is 6.5 m3. Calculate the volume of the ship.
Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are `(3)/(4)` times the corresponding sides of the ΔABC.
In a quadrilateral PQRS, the diagonals PR and QS intersect each other at the point T. If PT:TR = QT :TS = 1:2, show that TP:TQ = TR:TS
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆QMO

