Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are the midpoints of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.

उत्तर
It is given that D and E are midpoints of AB and AC.
Applying midpoint theorem, we can conclude that DE ‖ BC.
Hence, by B.P.T., we get :
`(AD)/(AB)=(AE)/(AC)`
Applying SAS similarity theorem, we can conclude that Δ ADE~ Δ ABC.
Therefore, the ration of areas of these triangles will be equal to the ratio of squares of their corresponding sides.
∴ `(9ar(ΔADE))/(ar(ΔABC))=(DE)^2/(BC)^2`
= `(1/2 BC)^2/(BC)^2`
= `1/4`
APPEARS IN
संबंधित प्रश्न
Examine each pair of triangles in Figure, and state which pair of triangles are similar. Also, state the similarity criterion used by you for answering the question and write the similarity relation in symbolic form
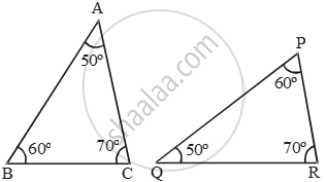
figure (i)
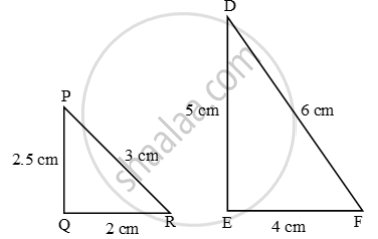
figure 2
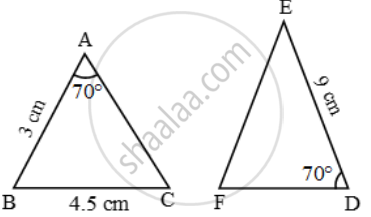
figure 3

figure 4
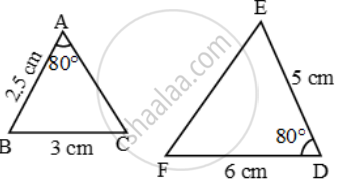
figure 5
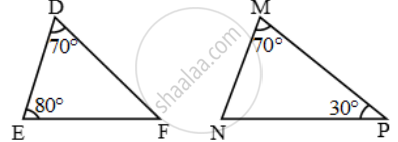
figure 6

figure 7
In figure, QA and PB are perpendicular to AB. If AO = 10 cm, BO = 6 cm and PB = 9 cm. Find AQ
In figure, ∠A = ∠CED, prove that ∆CAB ~ ∆CED. Also, find the value of x.

If a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse
See the given figure. DE || BC. Find EC.

Given `triangle ABC ~ triangle PQR`, if `(AB)/(PQ) = 1/3`, then find `(ar triangle ABC)/(ar triangle PQR)`
In the given figure, AB and DE are perpendicular to BC.

1) Prove that ΔABC ∼ ΔDEC
2) If AB = 6 cm; DE = 4 cm and AC = 15 cm. Calculate CD.
3) Find the ratio of area of ΔABC: area of ΔDEC
In the given figure, AB || EF || DC; AB = 67.5 cm, DC = 40.5 cm and AE = 52.5 cm.
- Name the three pairs of similar triangles.
- Find the lengths of EC and EF.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In an isosceles ΔABC, the base AB is produced both ways in P and Q such that
AP × BQ = AC2.
Prove that ΔACP~ΔBCQ.

The areas of two similar triangles are 169cm2 and 121cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
∆ABC and ∆DEF are equilateral triangles, A(∆ABC): A(∆DEF) = 1: 2. If AB = 4 then what is length of DE?

In the figure, parts of the two triangles bearing identical marks are
congruent. State the test by which the triangles are congruent.

In ΔPQR, PQ = 10 cm, QR = 12cm, PR = 8 cm, find the biggest and the smallest angle of the triangle.
Figure shows Δ PQR in which ST || QR and SR and QT intersect each other at M. If `"PT"/"TR" = 5/3` find `("Ar" (triangle "MTS"))/("Ar" (triangle "MQR"))`

A model of a ship is made with a scale factor of 1 : 500. Find
The deck area of the model, if the deck area of the ship is 1500000 m2
On a map drawn to a scale of 1 : 25000, a triangular plot of a land is marked as ABC with AB= 6cm, BC = 8cm and ∠ ABC = 90° . Calculate the actual length of AB in km and the actual area of the plot in km2 .
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of M' N', if MN = 8 cm.
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

In ΔABC, DE is parallel to BC and DE = 3:8.
Find:
(i) AD : BD
(ii) AE, if AC = 16.
Find the scale factor in each of the following and state the type of size transformation:
Model area = 75cm2, Actual area = 3cm2
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The diagonal distance of the plot in km
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN

A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
In the figure, which of the following statements is true?
Write the test of similarity for triangles given in figure.
Areas of two similar triangles are equal then prove that triangles are congruent
In ∠BAC = 90° and AD ⊥ BC. A then ______.

Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.
