Advertisements
Advertisements
प्रश्न
In an isosceles ΔABC, the base AB is produced both ways in P and Q such that
AP × BQ = AC2.
Prove that ΔACP~ΔBCQ.

उत्तर
Disclaimer: It should be ΔAPC ~ ΔBCQ instead of ΔACP ~
ΔBCQ
It is given that ΔABC is an isosceles triangle.
Therefore,
CA = CB
⟹ ∠𝐶𝐴𝐵 = ∠𝐶𝐵𝐴
⟹ 180°− ∠𝐶𝐴𝐵 = 180° − ∠𝐶𝐵𝐴
⟹ ∠𝐶𝐴𝑃 = ∠𝐶𝐵𝑄
Also,
`APxxBQ=AC^2`
⇒` (AP)/(AC)=(AC)/(BQ)`
⇒ `(AP)/(AC)=(BC)/(BQ)` (∵𝐴𝐶=𝐵𝐶 )
Thus, by SAS similarity theorem, we get
ΔAPC ~ ΔBCQ
This completes the proof.
APPEARS IN
संबंधित प्रश्न
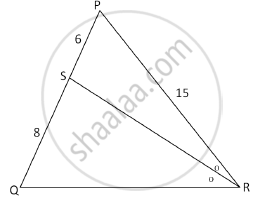
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
In figure, ∠BAC = 90º and segment AD ⊥ BC. Prove that AD2 = BD × DC.
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC in L and AD produced in E. Prove that EL = 2 BL
In the following figure, DE || OQ and DF || OR, show that EF || QR.

State, true or false:
Two isosceles-right triangles are similar.
In triangle ABC, DE is parallel to BC; where D and E are the points on AB and AC respectively.
Prove: ∆ADE ~ ∆ABC.
Also, find the length of DE, if AD = 12 cm, BD = 24 cm BC = 8 cm.
E and F are the points in sides DC and AB respectively of parallelogram ABCD. If diagonal AC
and segment EF intersect at G; prove that:
A line PQ is drawn parallel to the base BC of ∆ABC which meets sides AB and AC at points P and Q respectively. If AP = `1/3` PB; find the value of:
- `"Area of ΔABC"/"Area of ΔAPQ"`
- `"Area of ΔAPQ"/"Area of trapezium PBCQ"`
In the given figure, ΔOAB ~ ΔOCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
Select the appropriate alternative.
In ∆ABC and ∆PQR, in a one to one correspondence \[\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}\]

In the figure, parts of the two triangles bearing identical marks are
congruent. State the test by which the triangles are congruent.

Δ ABC ~ Δ DEF. If BC = 3cm , EF=4cm and area of Δ ABC = 54 cm2 , find area of Δ DEF.
In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`

On a map drawn to a scale of 1 : 25000, a triangular plot of a land is marked as ABC with AB= 6cm, BC = 8cm and ∠ ABC = 90° . Calculate the actual length of AB in km and the actual area of the plot in km2 .
The dimensions of the model of a multistorey building are 1.2 m × 75 cm × 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
DE = 2.4 cm, find the length of BC.

In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.

In the given figure, AB and DE are perpendicular to BC.

- Prove that ΔABC ∼ ΔDEC
- If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
- Find the ratio of the area of a ΔABC : area of ΔDEC.
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
In ΔABC, DE || BC such that AD =1.5 cm, DB = 3 cm and AE = 1 cm. Find AC.
Two figures are similar. If the ratio of their perimeters is 8:16. What will be the ratio of the corresponding sides?
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The length of a scale in km represented by 1cm on the map.
A model of a ship is made to a scale of 1:500. Find: The length of the ship, if length of the model is 1.2.
In the adjacent figure, ∆ABC is right angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE
In the adjacent figure ∠BAC = 90° and AD ⊥ BC then

If ΔABC ~ ΔLMN and ∠A = 60° then ∠L = ?
Areas of two similar triangles are equal then prove that triangles are congruent
In the figure PQ || BC. If `"PQ"/"BC" = 2/5` then `"AP"/"PB"` is ______.

