Advertisements
Advertisements
प्रश्न
Select the appropriate alternative.
In ∆ABC and ∆PQR, in a one to one correspondence \[\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}\]
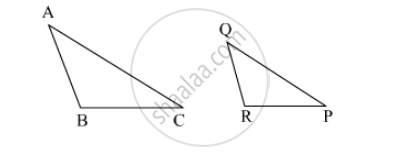
पर्याय
∆PQR ~ ∆ABC
∆PQR ~ ∆CAB
∆CBA ~ ∆PQR
∆BCA ~ ∆PQR
उत्तर
\[\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}\]
By SSS test of similarity
∆PQR ~ ∆CAB
Hence, the correct option is ∆PQR ~ ∆CAB.
संबंधित प्रश्न
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
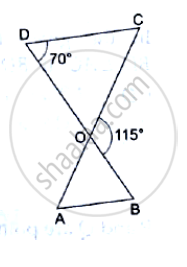
In the given figure, ΔODC~ΔOBA, ∠BOC = 115° and ∠CDO = 700.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.
P and Q are points on the sides AB and AC respectively of a ΔABC. If AP = 2cm, PB = 4cm, AQ = 3cm and QC = 6cm, show that BC = 3PQ.
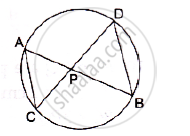
In a circle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a) ΔPAC ∼PDB (b) PA. PB= PC.PD
ΔABC ∼ ΔDEF and A(ΔABC) : A Δ(DEF) = 1 : 2 If AB = 4 find DE.
D and E are points on the sides AB and AC respectively of Δ ABC such that AB=5.6cm, AD= 1.4cm, AC=7 .2cm and AE = 1.5 cm, show that DE is parallel to BC
A model of a ship is made with a scale factor of 1 : 500. Find
The length of the ship, if the model length is 60 cm.
The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
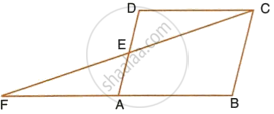
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.
In ΔABC, point D divides AB in the ratio 5:7, Find: DE, If BC = 4.8cm
In a right-angled triangle ABC, ∠B = 90°, P and Q are the points on the sides AB and AC such as PQBC, AB = 8 cm, AQ = 6 cm and PA:AB = 1:3. Find the lengths of AC and BC.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 8cm, Actual length = 20cm.
Find the scale factor in each of the following and state the type of size transformation:
Actual area = 64m2, Model area = 100cm2
Find the scale factor in each of the following and state the type of size transformation:
Model volume = 200cm3, Actual volume = 8cm3
Construct a triangle similar to a given triangle ABC with its sides equal to `6/5` of the corresponding sides of the triangle ABC (scale factor `6/5 > 1`)
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is
If ΔABC ~ ΔLMN and ∠A = 60° then ∠L = ?
Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non-parallel sides in the same ratio.
ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and point Q divides DC in the ratio 4:1. Prove that OC is half of OA.

