Advertisements
Advertisements
प्रश्न
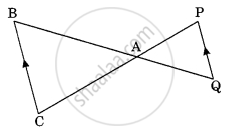
In the given figure 1.66, seg PQ || seg DE, A(∆PQF) = 20 units, PF = 2 DP, then Find A(◻DPQE) by completing the following activity.

उत्तर
Given:
seg PQ || seg DE
A(∆PQF) = 20 units
PF = 2 DP
Let us assume DP = x
∴ PF = 2x
\[DF = DP + PF = x + 2x = 3x\]
In △FDE and △FPQ
∠FDE = ∠FPQ (Corresponding angles)
∠FED = ∠FQP (Corresponding angles)
By AA test of similarity
△FDE ∼ △FPQ
\[\therefore \frac{A\left( \bigtriangleup FDE \right)}{A\left( \bigtriangleup FPQ \right)} = \frac{{FD}^2}{{FP}^2} = \frac{\left( 3x \right)^2}{\left( 2x \right)^2} = \frac{9}{4}\]
\[A\left( \bigtriangleup FDE \right) = \frac{9}{4}A\left( \bigtriangleup FPQ \right) = \frac{9}{4} \times 20 = 45\]
\[\therefore A\left( \square DPQE \right) = A\left( \bigtriangleup FDE \right) - A\left( \bigtriangleup FPQ \right)\]
\[ = 45 - 20\]
\[ = 25\]
संबंधित प्रश्न
If ∆ABC ~ ∆DEF such that area of ∆ABC is 16cm2 and the area of ∆DEF is 25cm2 and BC = 2.3 cm. Find the length of EF.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
In figure below ΔACB ~ ΔAPQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm,
find CA and AQ. Also, find the area (ΔACB): area (ΔAPQ)

Triangles ABC and DEF are similar If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the areas of ΔABC and ΔDEF.
ABC is a triangle in which ∠A =90°, AN⊥ BC, BC = 12 cm and AC = 5cm. Find the ratio of the areas of ΔANC and ΔABC.
In ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ΔABC into two parts equal in area. Find `(BP)/(AB)`
If D is a point on the side AB of ΔABC such that AD : DB = 3.2 and E is a Point on BC such that DE || AC. Find the ratio of areas of ΔABC and ΔBDE.
If ΔABC and ΔBDE are equilateral triangles, where D is the mid-point of BC, find the ratio of areas of ΔABC and ΔBDE.
Prove that the points (2, −2), (−2, 1) and (5, 2) are the vertices of a right angled triangle. Also find the area of this triangleb ?
If ∆ABC ~ ∆PQR, A (∆ABC) = 80, A (∆PQR) = 125, then fill in the blanks. \[\frac{A\left( ∆ ABC \right)}{A\left( ∆ . . . . \right)} = \frac{80}{125} \therefore \frac{AB}{PQ} = \frac{......}{......}\]
Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then Find corresponding side of the bigger triangle.
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that seg PQ || seg BC. If PQ divides ΔABC into two equal parts having equal areas, find `"BP"/"AB"`.
If ∆XYZ ~ ∆PQR and A(∆XYZ) = 25 cm2, A(∆PQR) = 4 cm2 then XY : PQ = ?
If ΔABC is similar to ΔDEF such that 2 AB = DE and BC = 8 cm then EF is equal to ______.
In the given figure, ΔACB ~ ΔAPQ. If AB = 6 cm, BC = 8 cm, and PQ = 4 cm then AQ is equal to ______.
In ΔABC, seg DE || side BC. If 2A(ΔADE) = A(⬜ DBCE), find AB : AD and show that BC = `sqrt(3)` DE.
