Advertisements
Advertisements
Question
In the given figure 1.66, seg PQ || seg DE, A(∆PQF) = 20 units, PF = 2 DP, then Find A(◻DPQE) by completing the following activity.

Solution
Given:
seg PQ || seg DE
A(∆PQF) = 20 units
PF = 2 DP
Let us assume DP = x
∴ PF = 2x
\[DF = DP + PF = x + 2x = 3x\]
In △FDE and △FPQ
∠FDE = ∠FPQ (Corresponding angles)
∠FED = ∠FQP (Corresponding angles)
By AA test of similarity
△FDE ∼ △FPQ
\[\therefore \frac{A\left( \bigtriangleup FDE \right)}{A\left( \bigtriangleup FPQ \right)} = \frac{{FD}^2}{{FP}^2} = \frac{\left( 3x \right)^2}{\left( 2x \right)^2} = \frac{9}{4}\]
\[A\left( \bigtriangleup FDE \right) = \frac{9}{4}A\left( \bigtriangleup FPQ \right) = \frac{9}{4} \times 20 = 45\]
\[\therefore A\left( \square DPQE \right) = A\left( \bigtriangleup FDE \right) - A\left( \bigtriangleup FPQ \right)\]
\[ = 45 - 20\]
\[ = 25\]
RELATED QUESTIONS
The areas of two similar triangles ∆ABC and ∆PQR are 25 cm2 and 49 cm2 respectively. If QR = 9.8 cm, find BC
If ∆ABC is similar to ∆DEF such that ∆DEF = 64 cm2 , DE = 5.1 cm and area of ∆ABC = 9 cm2 . Determine the area of AB
If ∆ABC ~ ∆DEF such that area of ∆ABC is 16cm2 and the area of ∆DEF is 25cm2 and BC = 2.3 cm. Find the length of EF.
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
If the areas of two similar triangles are equal, prove that they are congruent.
Triangles ABC and DEF are similar If AC = 19cm and DF = 8 cm, find the ratio of the area of two triangles.
In Figure, DE || BC If DE = 4 cm, BC = 6 cm and Area (ΔADE) = 16 cm2, find the area of ΔABC.
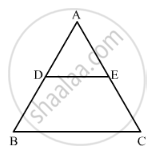
In ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC
The areas of two similar triangles are 100 cm2 and 49 cm2 respectively. If the altitude the bigger triangle is 5 cm, find the corresponding altitude of the other.
The ratio of corresponding sides of similar triangles is 3 : 5; then find the ratio of their areas.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that seg PQ || seg BC. If PQ divides ΔABC into two equal parts having equal areas, find `"BP"/"AB"`.
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
If ∆XYZ ~ ∆PQR and A(∆XYZ) = 25 cm2, A(∆PQR) = 4 cm2 then XY : PQ = ?
In ΔLMN, ∠L = 50° and ∠N = 60°, If ΔLMN ~ ΔPQR, then find ∠Q.
O is a point on side PQ of a APQR such that PO = QO = RO, then ______.
In a rectangle Length = 8 cm, Breadth = 6 cm. Then its diagonal = ______.
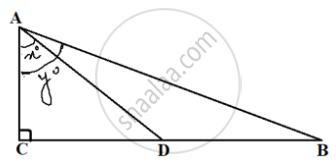
In the given figure, D is the mid-point of BC, then the value of `(coty^circ)/(cotx^circ)` is ______.
If ΔABC ~ ΔPQR, AB : PQ = 4 : 5 and A(ΔPQR) = 125 cm2, then find A(ΔABC).
