Question

D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.

Answer 1

Since D and E are the mid-points of the sides BC and AB respectively of ∆ABC. Therefore,

DE || BA

DE || FA  ... (i)

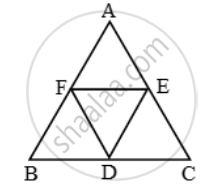
Since D and F are mid-points of the sides BC and AB respectively of ∆ABC. Therefore,

DF || CA ⇒ DF || AE

From (i), and (ii), we conclude that AFDE is a parallelogram.

Similarly, BDEF is a parallelogram.

Now, in ∆DEF and ∆ABC, we have

∠FDE = ∠A [Opposite angles of parallelogram AFDE] and, ∠DEF = ∠B [Opposite angles of parallelogram BDEF]

So, by AA-similarity criterion, we have ∆DEF ~ ∆ABC

`\Rightarrow \frac{Area\ (\Delta DEF)}{Area\ (\Delta ABC)}=(DE^2)/(AB^2)=(` [∵ DE = 1/2AB]

Hence, Area (DDEF) : Area (DABC) = 1 : 4.