Advertisements
Advertisements
Question
If the areas of two similar triangles are equal, prove that they are congruent.
Solution
Let us assume two similar triangle as ΔABC ~ ΔPQR
`(ar(triangleABC))/(ar(trianglePQR))=((AB)/(PQ))^2 = ((BC)/(QR))^2=((AC)/(PR))^2 ...(1)`
Given that, ar(ΔABC) = ar(ΔABC)
`=>(ar(triangleABC))/(ar(trianglePQR)) =1`
Putting this value in equation (1) we obtain
`1=((AB)/(PQ))^2= ((BC)/(QR))^2=((AC)/(PR))^2`
⇒ AB = PQ, BC = QR and AC = PR
∴ ΔABC ≅ ΔPQR (By SSS congruence criterion)
APPEARS IN
RELATED QUESTIONS
In a trapezium ABCD, O is the point of intersection of AC and BD, AB || CD and AB = 2 × CD. If the area of ∆AOB = 84 cm2 . Find the area of ∆COD
The areas of two similar triangles are 81 cm2 and 49 cm2 respectively. Find the ratio of their corresponding heights. What is the ratio of their corresponding medians?
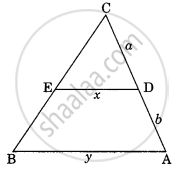
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ΔABC into two parts equal in area. Find `(BP)/(AB)`
The ratio of corresponding sides of similar triangles is 3 : 5, then find the ratio of their areas.
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
In the given figure DE || AC which of the following is true?
In ΔLMN, ∠L = 50° and ∠N = 60°, If ΔLMN ~ ΔPQR, then find ∠Q.
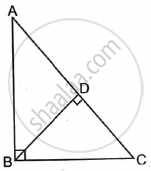
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.
If ΔPQR ∼ ΔABC; PQ = 6 cm, AB = 8 cm and the perimeter of ΔABC is 36 cm, then the perimeter of ΔPQR is ______.
