Advertisements
Advertisements
प्रश्न
If the areas of two similar triangles are equal, prove that they are congruent.
उत्तर
Let us assume two similar triangle as ΔABC ~ ΔPQR
`(ar(triangleABC))/(ar(trianglePQR))=((AB)/(PQ))^2 = ((BC)/(QR))^2=((AC)/(PR))^2 ...(1)`
Given that, ar(ΔABC) = ar(ΔABC)
`=>(ar(triangleABC))/(ar(trianglePQR)) =1`
Putting this value in equation (1) we obtain
`1=((AB)/(PQ))^2= ((BC)/(QR))^2=((AC)/(PR))^2`
⇒ AB = PQ, BC = QR and AC = PR
∴ ΔABC ≅ ΔPQR (By SSS congruence criterion)
APPEARS IN
संबंधित प्रश्न
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals
In Figure, DE || BC If DE = 4cm, BC = 8 cm and Area (ΔADE) = 25 cm2, find the area of ΔABC.
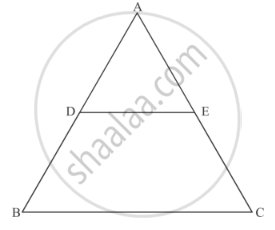
In ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC
If ∆ABC ~ ∆PQR and AB : PQ = 2 : 3, then fill in the blanks.
\[\frac{A\left( ∆ ABC \right)}{A\left( ∆ PQR \right)} = \frac{{AB}^2}{......} = \frac{2^2}{3^2} = \frac{......}{.......}\]
The ratio of corresponding sides of similar triangles is 3 : 5, then find the ratio of their areas.
If ΔABC is similar to ΔDEF such that 2 AB = DE and BC = 8 cm then EF is equal to ______.
In ΔLMN, ∠L = 50° and ∠N = 60°, If ΔLMN ~ ΔPQR, then find ∠Q.
In a rectangle Length = 8 cm, Breadth = 6 cm. Then its diagonal = ______.
