Advertisements
Advertisements
प्रश्न
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
उत्तर
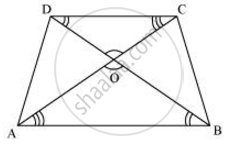
Since AB || CD,
∴ ∠OAB = ∠OCD and ∠OBA = ∠ODC (Alternate interior angles)
In ΔAOB and ΔCOD,
∠AOB = ∠COD (Vertically opposite angles)
∠OAB = ∠OCD (Alternate interior angles)
∠OBA = ∠ODC (Alternate interior angles)
∴ ΔAOB ∼ ΔCOD (By AAA similarity criterion)
`:.(ar(ΔAOB))/(ar(COD)) = ((AB)/(CD))^2`
Since AB = 2 CD
`:. (ar(triangleAOB))/(ar(triangleCOD)) =((2CD)/(CD))^2 =4/1=4:1`
APPEARS IN
संबंधित प्रश्न
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
If the areas of two similar triangles are equal, prove that they are congruent.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
Prove that the points (2, −2), (−2, 1) and (5, 2) are the vertices of a right angled triangle. Also find the area of this triangleb ?
If ΔABC is similar to ΔDEF such that 2 AB = DE and BC = 8 cm then EF is equal to ______.
If ΔABC ~ ΔPQR, AB : PQ = 4 : 5 and A(ΔPQR) = 125 cm2, then find A(ΔABC).
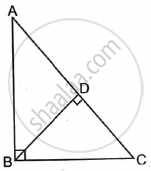
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.
Use area theorem of similar triangles to prove congruency of two similar triangles with equal areas.
If ΔPQR ∼ ΔABC; PQ = 6 cm, AB = 8 cm and the perimeter of ΔABC is 36 cm, then the perimeter of ΔPQR is ______.
