Advertisements
Advertisements
Question
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
Solution
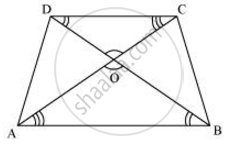
Since AB || CD,
∴ ∠OAB = ∠OCD and ∠OBA = ∠ODC (Alternate interior angles)
In ΔAOB and ΔCOD,
∠AOB = ∠COD (Vertically opposite angles)
∠OAB = ∠OCD (Alternate interior angles)
∠OBA = ∠ODC (Alternate interior angles)
∴ ΔAOB ∼ ΔCOD (By AAA similarity criterion)
`:.(ar(ΔAOB))/(ar(COD)) = ((AB)/(CD))^2`
Since AB = 2 CD
`:. (ar(triangleAOB))/(ar(triangleCOD)) =((2CD)/(CD))^2 =4/1=4:1`
APPEARS IN
RELATED QUESTIONS
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
Triangles ABC and DEF are similar If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
Triangles ABC and DEF are similar If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the areas of ΔABC and ΔDEF.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
In ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC
Prove that the points (2, −2), (−2, 1) and (5, 2) are the vertices of a right angled triangle. Also find the area of this triangleb ?
O is a point on side PQ of a APQR such that PO = QO = RO, then ______.
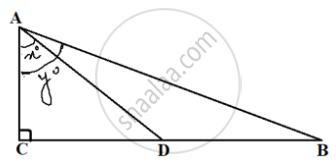
In the given figure, D is the mid-point of BC, then the value of `(coty^circ)/(cotx^circ)` is ______.
Find the length of ST, if ΔPQR ∼ ΔPST.

