Advertisements
Advertisements
Question
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
Solution
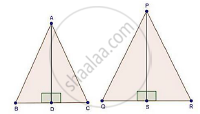
We have,
ΔABC ~ ΔPQR
AD = 6 cm
And, PS = 9 cm
By area of similar triangle theorem
`("Area"(triangleABC))/("Area"(trianglePQR))="AB"^2/"PQ"^2` ........(i)
In ΔABD and ΔPQS
∠B = ∠Q [ΔABC ~ ΔPQR]
∠ADB = ∠PSQ [Each 90°]
Then, ΔABD ~ ΔPQS [By AA similarity]
`therefore"AB"/"PQ"="AD"/"PS"` [Corresponding parts of similar Δ are proportional]
`rArr"AB"/"PQ"=6/9`
`rArr"AB"/"PQ"=2/3` ......(ii)
Compare equations (i) and (ii)
`("Area"(triangleABC))/("Area"(trianglePQR))=(2/3)^2=4/9`
APPEARS IN
RELATED QUESTIONS
In two similar triangles ABC and PQR, if their corresponding altitudes AD and PS are in the ratio 4 : 9, find the ratio of the areas of ∆ABC and ∆PQR
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
If the areas of two similar triangles are equal, prove that they are congruent.
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
The areas of two similar triangles are 100 cm2 and 49 cm2 respectively. If the altitude the bigger triangle is 5 cm, find the corresponding altitude of the other.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ΔABC into two parts equal in area. Find `(BP)/(AB)`
If ΔABC and ΔBDE are equilateral triangles, where D is the mid-point of BC, find the ratio of areas of ΔABC and ΔBDE.
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area (ΔADE): Area (ΔABC) = 3: 4
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
Use area theorem of similar triangles to prove congruency of two similar triangles with equal areas.
