Advertisements
Advertisements
Question
If ΔABC and ΔBDE are equilateral triangles, where D is the mid-point of BC, find the ratio of areas of ΔABC and ΔBDE.
Solution
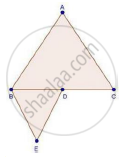
We have,
ΔABC and ΔBDE are equilateral triangles then both triangles are equiangular
∴ ΔABC ~ ΔBDE [By AAA similarity]
By area of similar triangle theorem
`("area"(triangleABC))/("area"(triangleBDE))="BC"^2/"BD"^2`
`=(2"BD")^2/"BD"^2` [D is the mid-point of BC]
`=(4"BD"^2)/"BD"^2`
`=4/1`
APPEARS IN
RELATED QUESTIONS
In two similar triangles ABC and PQR, if their corresponding altitudes AD and PS are in the ratio 4 : 9, find the ratio of the areas of ∆ABC and ∆PQR
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
ABC is a triangle in which ∠A =90°, AN⊥ BC, BC = 12 cm and AC = 5cm. Find the ratio of the areas of ΔANC and ΔABC.
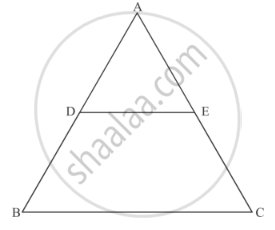
In Figure, DE || BC If DE = 4cm, BC = 8 cm and Area (ΔADE) = 25 cm2, find the area of ΔABC.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ΔABC into two parts equal in area. Find `(BP)/(AB)`
Ratio of areas of two similar triangles is 9 : 25. _______ is the ratio of their corresponding sides.
In the given figure, ΔACB ~ ΔAPQ. If AB = 6 cm, BC = 8 cm, and PQ = 4 cm then AQ is equal to ______.
In ΔLMN, ∠L = 50° and ∠N = 60°, If ΔLMN ~ ΔPQR, then find ∠Q.
If ΔABC ~ ΔPQR, AB : PQ = 4 : 5 and A(ΔPQR) = 125 cm2, then find A(ΔABC).
