Advertisements
Advertisements
Question
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area (ΔADE): Area (ΔABC) = 3: 4
Solution
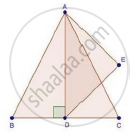
We have,
ΔABC is an equilateral triangle
Then, AB = BC = AC
Let, AB = BC = AC = 2x
Since, AD ⊥ BC then BD = DC = x
In ΔADB, by Pythagoras theorem
𝐴𝐵2 = (2𝑥)2 − (𝑥)2
⇒ 𝐴𝐷2 = 4𝑥2 − 𝑥2 = 3𝑥2
⇒ 𝐴𝐷 = `sqrt3`𝑥 cm
Since, ΔABC and ΔADE both are equilateral triangles then they are equiangular
∴ ΔABC ~ ΔADE [By AA similarity]
By area of similar triangle theorem
`("area"(triangleADE))/("area"(triangleABC))="AD"^2/"AB"^2`
`=(sqrt3x)^2/(2x)^2`
`=(3x^2)/(4x^2)`
`=3/4`
APPEARS IN
RELATED QUESTIONS
D, E, F are the mid-point of the sides BC, CA and AB respectively of a ∆ABC. Determine the ratio of the areas of ∆DEF and ∆ABC.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the area of ΔDEF and ΔABC.
Triangles ABC and DEF are similar If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, find the length of QR.
If ∆ABC ~ ∆PQR, A (∆ABC) = 80, A (∆PQR) = 125, then fill in the blanks. \[\frac{A\left( ∆ ABC \right)}{A\left( ∆ . . . . \right)} = \frac{80}{125} \therefore \frac{AB}{PQ} = \frac{......}{......}\]
The perpendicular from A on side BC of a Δ ABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2.
In ΔLMN, ∠L = 50° and ∠N = 60°, If ΔLMN ~ ΔPQR, then find ∠Q.
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.