Advertisements
Advertisements
Question
D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the area of ΔDEF and ΔABC.
Solution

D and E are the mid-points of ΔABC
:.DE || AC and DE = `1/2AC`
In ΔBED and ΔBCA
∠BED = ∠BCA (Corresponding angle)
∠BDE = ∠BAC (Corresponding angle)
∠EBD = ∠CBA (Common angles)
∴ΔBED ~ ΔBCA (AAA similarity criterion)
`(ar(ΔBED))/(ar(ΔBCA)) = 1/4`
`=>ar(ΔBED) = 1/4 ar(ΔBCA)`
Similary
`ar(ΔCFE) = 1/4ar(CBA) `
Also ar(ΔDEF) = ar(ΔABC) - [ar(ΔBED) + ar(ΔCFE) + ar(ΔADF)]
`=>ar(ΔDEF) = ar(ΔABC) - 3/4 ar(ΔABC) = 1/4 ar(ΔABC)`
`=>ar(ΔDEF) = ar(ΔABC) - 3/4 ar(ΔABC) = 1/4 ar(ΔABC)`
`=>(ar(ΔDEF))/(ar(ΔABC)) = 1/4`
APPEARS IN
RELATED QUESTIONS
D and E are points on the sides AB and AC respectively of a ∆ABC such that DE || BC and divides ∆ABC into two parts, equal in area. Find
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that: (i) ΔAOB and ΔCOD (ii) If OA = 6 cm, OC = 8 cm,
Find:(a) `("area"(triangleAOB))/("area"(triangleCOD))`
(b) `("area"(triangleAOD))/("area"(triangleCOD))`
In ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other.
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 m, prove that area of ΔAPQ is one- sixteenth of the area of ABC.
O is a point on side PQ of a APQR such that PO = QO = RO, then ______.
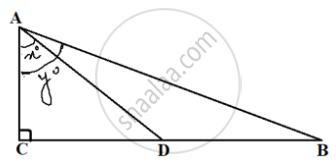
In the given figure, D is the mid-point of BC, then the value of `(coty^circ)/(cotx^circ)` is ______.
ΔABC ~ ΔPQR. In ΔABC, AB = 5.4 cm, BC = 4.2 cm, AC = 6.0 cm, AB:PQ = 3:2, then construct ΔABC and ΔPQR.
If ΔABC ∼ ΔPQR and `(A(ΔABC))/(A(ΔPQR)) = 16/25`, then find AB : PQ.
