Advertisements
Advertisements
Question
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution
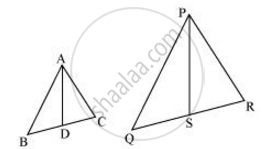
Let us assume two similar triangles as ΔABC ∼ ΔPQR. Let AD and PS be the medians of these triangles.
∵ ΔABC ∼ ΔPQR
:.(AB)/(PQ) = (BC)/(QR) = (AC)/(PR)...(1)
∠A = ∠P, ∠B = ∠Q, ∠C = ∠R … (2)
Since AD and PS are medians,
∴ BD = DC = `(BC)/2`
And, QS = SR = `(QR)/2`
Equation (1) becomes
(AB)/(PQ) = (BD)/(QS) = (AC)/(PR) ....(3)
In ΔABD and ΔPQS,
∠B = ∠Q [Using equation (2)]
and (AB)/(PQ) = (BD)/(QS) [Using equation (3)]
∴ ΔABD ∼ ΔPQS (SAS similarity criterion)
Therefore, it can be said that
`(AB)/(PQ) = (BD)/(QS) =(AD)/(PS) ....(4)`
`(ar(triangleABC))/(ar(trianglePQR)) = ((AB)/(PQ))^2 = ((BC)/(QR))^2 = ((AC)/(PR))^2`
From equations (1) and (4), we may find that
`(AB)/(PQ) = (BC)/(QR) = (AC)/(PR) = (AD)/(PS)`
And hence
`(ar(triangleABC))/(ar(trianglePQR)) = ((AD)/(PS))^2`
APPEARS IN
RELATED QUESTIONS
If the areas of two similar triangles are equal, prove that they are congruent.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals
ABC is a triangle in which ∠A =90°, AN⊥ BC, BC = 12 cm and AC = 5cm. Find the ratio of the areas of ΔANC and ΔABC.
In ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, find the length of QR.
If ∆ABC ~ ∆PQR, A (∆ABC) = 80, A (∆PQR) = 125, then fill in the blanks. \[\frac{A\left( ∆ ABC \right)}{A\left( ∆ . . . . \right)} = \frac{80}{125} \therefore \frac{AB}{PQ} = \frac{......}{......}\]
Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then Find corresponding side of the bigger triangle.
∆ABC and ∆DEF are equilateral triangles. If A(∆ABC) : A(∆DEF) = 1 : 2 and AB = 4, find DE.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that seg PQ || seg BC. If PQ divides ΔABC into two equal parts having equal areas, find `"BP"/"AB"`.
If ΔABC is similar to ΔDEF such that 2 AB = DE and BC = 8 cm then EF is equal to ______.
