Advertisements
Advertisements
Question
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, find the length of QR.
Solution
We have,
ΔABC ~ ΔPQR
`("area"(triangleABC))/("area"(trianglePQR))="BC"^2/"QR"^2`
`rArr9/16=4.5^2/"QR"^2`
`rArr3/4=4.5/"QR"` [Taking square root]
`rArr"QR"=(4xx4.5)/3=6` cm
APPEARS IN
RELATED QUESTIONS
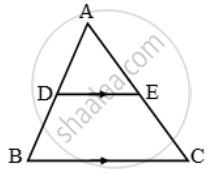
In the given figure, DE || BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED
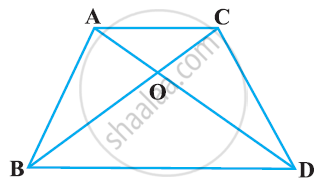
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that `(ar(ABC))/(ar(DBC)) = (AO)/(DO)`
Triangles ABC and DEF are similar If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
∆MNT ~ ∆QRS. Length of altitude drawn from point T is 5 and length of altitude drawn from point S is 9. Find the ratio `("A"(Δ"MNT"))/("A"(Δ"QRS"))`.
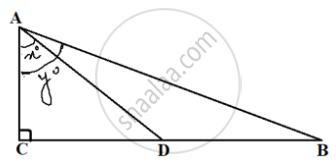
In the given figure, D is the mid-point of BC, then the value of `(coty^circ)/(cotx^circ)` is ______.
Use area theorem of similar triangles to prove congruency of two similar triangles with equal areas.
If ΔABC ∼ ΔPQR and `(A(ΔABC))/(A(ΔPQR)) = 16/25`, then find AB : PQ.
In ΔABC, seg DE || side BC. If 2A(ΔADE) = A(⬜ DBCE), find AB : AD and show that BC = `sqrt(3)` DE.
If ΔABC ∼ ∆PQR and AB : PQ = 2 : 3, then find the value of `(A(triangleABC))/(A(trianglePQR))`.
