Advertisements
Advertisements
प्रश्न
D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the area of ΔDEF and ΔABC.
उत्तर

D and E are the mid-points of ΔABC
:.DE || AC and DE = `1/2AC`
In ΔBED and ΔBCA
∠BED = ∠BCA (Corresponding angle)
∠BDE = ∠BAC (Corresponding angle)
∠EBD = ∠CBA (Common angles)
∴ΔBED ~ ΔBCA (AAA similarity criterion)
`(ar(ΔBED))/(ar(ΔBCA)) = 1/4`
`=>ar(ΔBED) = 1/4 ar(ΔBCA)`
Similary
`ar(ΔCFE) = 1/4ar(CBA) `
Also ar(ΔDEF) = ar(ΔABC) - [ar(ΔBED) + ar(ΔCFE) + ar(ΔADF)]
`=>ar(ΔDEF) = ar(ΔABC) - 3/4 ar(ΔABC) = 1/4 ar(ΔABC)`
`=>ar(ΔDEF) = ar(ΔABC) - 3/4 ar(ΔABC) = 1/4 ar(ΔABC)`
`=>(ar(ΔDEF))/(ar(ΔABC)) = 1/4`
APPEARS IN
संबंधित प्रश्न
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half the area of the similar Triangle ACF described on the diagonal AC as base
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, find the longest side of the smaller triangle.
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ΔABC into two parts equal in area. Find `(BP)/(AB)`
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, find the length of QR.
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that seg PQ || seg BC. If PQ divides ΔABC into two equal parts having equal areas, find `"BP"/"AB"`.
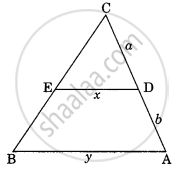
In the given figure DE || AC which of the following is true?
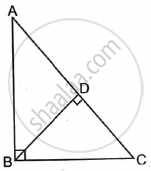
In the adjoining figure, ΔADB ∼ ΔBDC. Prove that BD2 = AD × DC.
If the perimeter of two similar triangles is in the ratio 2 : 3, what is the ratio of their sides?
