Advertisements
Advertisements
प्रश्न
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
उत्तर
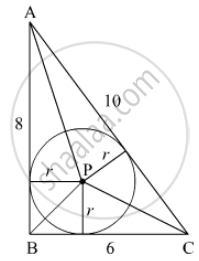
We have given that a circle is inscribed in a triangle
Using pythagoras theorem
(AC)2 = (AB)2 + (BC)2
(AC)2 = (8)2 + (6)2
(AC)2 = 64 + 36
(AC)2 = 100
⇒ AC = 10
Area of △ABC = area of △APB + area of △BPC + area of △APC
`1/2 xx b xx h = 1/2 xx b_1 xx h_1 + 1/2 xx b_2 xx h_2 + 1/2 xx b_3 xx h_3`
`1/2 xx 6 xx 8 = 1/2 xx 8 xx r + 12 xx 6 xx r + 12 xx 10 xx r`
24 = 4r + 3r + 5r
24 = 12r
⇒ r = 2
∵ d = 2r
⇒ d = 2 x 2
⇒ d = 4 cm.
APPEARS IN
संबंधित प्रश्न
In two similar triangles ABC and PQR, if their corresponding altitudes AD and PS are in the ratio 4 : 9, find the ratio of the areas of ∆ABC and ∆PQR
If ∆ABC ~ ∆DEF such that area of ∆ABC is 16cm2 and the area of ∆DEF is 25cm2 and BC = 2.3 cm. Find the length of EF.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
In ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
Areas of two similar triangles are 225 sq.cm. 81 sq.cm. If a side of the smaller triangle is 12 cm, then Find corresponding side of the bigger triangle.
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
Use area theorem of similar triangles to prove congruency of two similar triangles with equal areas.
Find the length of ST, if ΔPQR ∼ ΔPST.

If the perimeter of two similar triangles is in the ratio 2 : 3, what is the ratio of their sides?
